Absorbtion
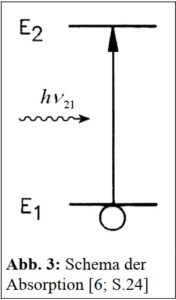 Wird ein Atom, das sich in dem unteren Energiezustand E1 befindet, von einem Photon getroffen, so ist es möglich, dass das Atom die gesamte Energie des Lichtquants aufnimmt, das heißt absorbiert, und das Photon auf diese Weise vernichtet.
Wird ein Atom, das sich in dem unteren Energiezustand E1 befindet, von einem Photon getroffen, so ist es möglich, dass das Atom die gesamte Energie des Lichtquants aufnimmt, das heißt absorbiert, und das Photon auf diese Weise vernichtet.
Durch die aufgenommene Energie geht das Atom in einen höheren Energiezustand E2 über. Die Wahrscheinlichkeit für diesen Vorgang steigt mit wachsender Übereinstimmung der Energie des Photons E = h ν mit der Energiedifferenz E12 der beiden atomaren Zustände E2 und E1:
∆E12 = E2 − E1
Demnach ist die Absorptionswahrscheinlichkeit genau dann am größten, wenn die Energie des Photons gleich dieser Energiedifferenz ∆E12 ist. Dies ist der Fall, wenn das Lichtquant die Resonanzfrequenz 21 des Atoms besitzt
ν21 = ∆E12 / h
Darüber hinaus hängt die Wahrscheinlichkeit für einen Absorptionsprozess von der Anzahl N1 der im unteren Energieniveau befindlichen Atome und der spektralen Energiedichte ρ(21) (Energie pro Volumen- und Frequenzeinheit bei der Resonanzfrequenz) ab. Die spektrale Energiedichte bezeichnet die „Energiedichte des Strahlungsfeldes in der Umgebung der Resonanzfrequenz“. Wenn wir nun die Zahl der Atome, die pro Zeiteinheit ein Photon absorbieren und in das Energieniveau E2 übergehen, betrachten, ergibt sich für deren Übergangsrate
dN1 / dt = -B12 N1 ρ(ν21 )
wobei es sich bei B12 um einen vom betrachteten System abhängigen Proportionalitätsfaktor handelt. Er heißt Einstein-Koeffizient der induzierten Absorption. Das negative Vorzeichen in der Gleichung erklärt sich aus der Tatsache, dass durch Absorption die Atome angeregt werden und daher das untere Energieniveau
verlassen.