Fibonacci-Folge

• Wikipedia-de: Fibonacci-Folge

Die Fibonacci-Folge ist die unendliche Folge natürlicher Zahlen, die (ursprünglich) mit zweimal der Zahl 1 beginnt oder (häufig, in moderner Schreibweise) zusätzlich mit einer führenden Zahl 0 versehen ist.^[1] Im Anschluss ergibt jeweils die Summe zweier aufeinanderfolgender Zahlen die unmittelbar danach folgende Zahl:

Die darin enthaltenen Zahlen heißen Fibonacci-Zahlen. Benannt ist die Folge nach Leonardo Fibonacci, der damit im Jahr 1202 das Wachstum einer Kaninchenpopulation beschrieb. Die Folge war aber schon in der Antike sowohl den Griechen als auch den Indern bekannt.

Weitere Untersuchungen zeigten, dass die Fibonacci-Folge auch noch zahlreiche andere Wachstumsvorgänge in der Natur beschreibt. Es scheint, als sei sie eine Art Wachstumsmuster in der Natur.

Die Fibonacci-Zahlen weisen einige bemerkenswerte mathematische Besonderheiten auf:

• Aufgrund der Beziehung zur vorherigen und zur folgenden Zahl scheint Wachstum in der Natur einem Additionsgesetz zu folgen.
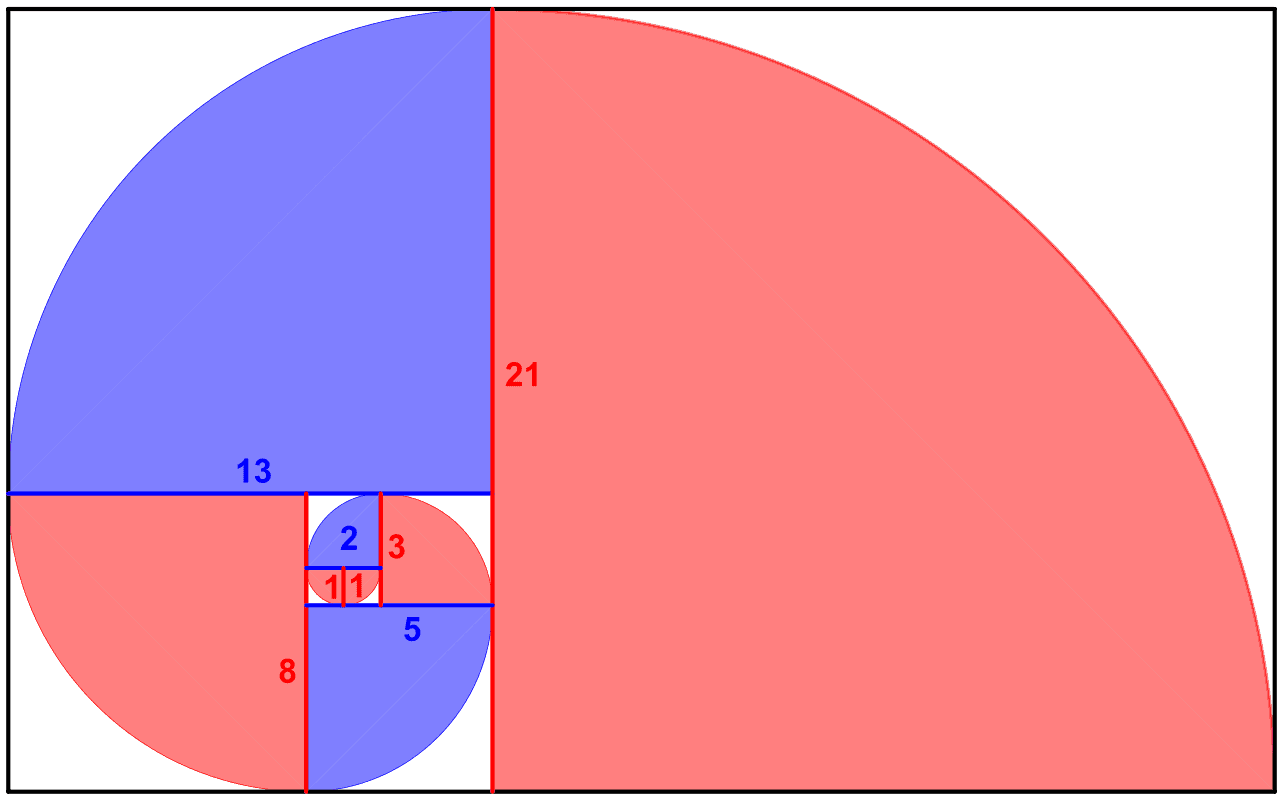
• Die Fibonacci-Folge steht in einem unmittelbaren Zusammenhang zum Goldenen Schnitt. Je weiter man in der Folge fortschreitet, desto mehr nähert sich der Quotient aufeinanderfolgender Zahlen dem Goldenen Schnitt (1,618033…) an (beispielsweise 13:8 = 1,6250; 21:13 ≈ 1,6154; 34:21 ≈ 1,6190; 55:34 ≈ 1,6176; etc.).
• Diese Annäherung ist alternierend, d. h., die Quotienten sind abwechselnd kleiner und größer als der Goldene Schnitt.