Raffiniert ist der Herrgott "Verbogene Raum-Zeit" von Harald Fritsch
Raffiniert ist der Herrgott, aber boshaft ist er nicht… Die Natur verbirgt ihr Geheimnis durch die Erhabenheit ihres Wesens, aber nicht durch List..
Albert Einstein

Kurz nach 7 Uhr stand Haller auf. Das Klappern von Geschirr aus der Küche hatte ihn aufgeweckt. Dort wurde das Frühstück für die Gäste zubereitet. Eine halbe Stunde später saßen Einstein und Haller am Tisch im Wohnzimmer. Einstein erinnerte sich an die vielen angenehmen Tage, die er vor langer Zeit hier verbracht hatte. »Das Beste war das Segeln, vor allem, wenn man von aller Welt gesucht wurde. Am liebsten hatte ich es, wenn der Wind für Stunden ausblieb und ich mit dem Boot irgendwo auf dem Wasser trieb, unerreichbar. Dann hatte ich alle Zeit der Welt zum Nachdenken.«
»Ich würde vorschlagen, daß wir unsere Diskussion irgendwann auch mal beim Segeln durchführen«, sagte Newton, der mittlerweile in der Tür erschienen war. »Ok – wollen wir das mal vormerken. Aber jetzt nehmen Sie erst mal Platz.
Wir können ja schon beim Frühstück mit unserem Geschäft anfangen. Schießen Sie los, Sir Isaac – es geht heute um Raum, Zeit und Gravitation.«
Newton: Wie ich kürzlich las, behaupten Sie ja, daß es möglich ist, die Gravitation mit Hilfe Ihrer Relativitätstheorie zu verstehen, Mr. Einstein. Dann müßte man doch eigentlich sagen: Raum-Zeit und Gravitation, denn schließlich werden Raum und Zeit im Rahmen Ihrer Relativitätstheorie zu einer Einheit zusammengefügt, und ich darf wohl annehmen, daß Sie dies nicht wieder rückgängig machen wollen.
Einstein: Also gut, wenn Sie wollen, können wir durchaus auch Raum-Zeit oder Zeit-Raum sagen, aber das ist im Grunde gar nicht so wichtig. Worauf es mir ankommt: Raum, Zeit und Gravitationskraft sind so eng miteinander verknüpft, daß man diese drei Aspekte unseres Universums fast als drei verschiedene Seiten ein und desselben Sachverhalts ansehen kann.
Newton (erhob sich kopfschüttelnd und warf Einstein einen mißbilligenden Blick zu): Nicht so schnell, Herr Kollege. In Ihrer Relativitätstheorie, genauer in der, wie man wohl heute sagt, Speziellen Relativitätstheorie, haben Sie ja gezeigt, daß es einen absoluten Raum und eine absolute Zeit in unserem Universum nicht gibt, nicht geben kann. Vielmehr hängen der Zeitablauf und die Eigenschaften des Raumes vom Bezugssystem ab, also vom jeweiligen Beobachter. Zwei verschiedene Beobachter, die sich relativ zueinander mit gleichförmiger Geschwindigkeit bewegen, beobachten zwei Ereignisse im Raum ja in verschiedener Weise. Beispielsweise stellen sie fest, daß der zeitliche Abstand zwischen
Abb. 3-1 Einstein am Ruder seines Bootes »Tümmler«. (Foto Hermann Landshoff, 1930)
zwei Ereignissen für sie beide nicht gleich ist. Das alles habe ich ja akzeptiert, auch wenn es mich, wie Sie wissen, viel Mühe und Überwindung gekostet hat, meine Ideen des absoluten Raumes und der absoluten Zeit über Bord zu werfen. Ich weiß auch, daß die Relativitätstheorie neue Aspekte der Kräfte in der Natur beleuchtet. So kann man, wie wir gesehen haben, die elektrischen und die magnetischen Kräfte nicht als losgelöst voneinander betrachten, wie das am Anfang der Entwicklung der Elektrizitätslehre der Fall gewesen war – relativistisch gesehen gibt es nur eine, die elektrodynamische Kraft.
Haller: Richtig – ein elektrisches Kraftfeld, etwa das einer elektrisch geladenen Metallkugel, ist kein reines elektrisches Feld mehr, wenn man es von einem bewegten Bezugssystem aus betrachtet, sondern wird von einem magnetischen Kraftfeld begleitet.
Newton: Ja, das habe ich mir mittlerweile auch klargemacht. Ein elektrischer Strom, der durch einen Draht fließt, erzeugt um den Draht ein magnetisches Kraftfeld, das letztlich von der Tatsache herrührt, daß der elektrische Strom aus vielen Elektronen besteht, die sich in dem Draht bewegen. Durch diese Bewegung wird ein magnetisches Feld erzeugt. Es ist also letztlich eine Folge der Relativitätstheorie. Was ich jedoch meine, ist die Tatsache, daß elektrische und magnetische Felder in der Natur vorgegebene Kraftfelder sind, die zunächst einmal nichts mit der Relativitätstheorie zu tun haben. Die Physiker im letzten Jahrhundert konnten ja mit den elektrischen und magnetischen Erscheinungen ganz gut umgehen, auch wenn sie keine Ahnung von der Relativitätstheorie hatten. Betrachten wir zwei elektrisch geladene Kugeln, die eine positiv, die andere negativ. Ungleichnamige Ladungen ziehen sich an, also herrscht zwischen den beiden Kugeln eine attraktive Kraft, deren Stärke davon abhängt, wie groß der Abstand zwischen den beiden Kugeln ist. Je größer der Abstand, um so schwächer die Kraft, die ja mit dem Quadrat des Abstandes abnimmt – verdopple ich die Distanz, nimmt die Kraft um das Vierfache ab. Dieses einfache Kraftgesetz ist selbstverständlich keine direkte Folge der Relativitätstheorie, auch wenn letztere die elektrische Kraft in einem, wie ich meine, neuen und interessanten Licht beleuchtet. Für die Gravitationskraft könnte dies jedoch ebenso zutreffen. Um das gerade zitierte Beispiel mit den zwei Kugeln zu verwenden: Wenn wir die Ladungen auf den beiden Kugeln entfernen, gibt es zwischen ihnen selbstverständlich keine elektrische Anziehung mehr, jedoch bleibt die Gravitation, also die Massenanziehung zwischen den beiden Kugeln, erhalten. Beide ziehen sich an, wobei die Kraft um so stärker ist, je größer die Massen der Metallkugeln sind. Auch bei der Massenanziehung gilt ja, wie wir wissen: Je größer der Abstand, um so geringer die Kraft, die auch hier mit dem Quadrat der Entfernung abfällt. Mein Kraftgesetz der Gravitation ist ja ganz ähnlich dem Kraftgesetz der Elektrizitätslehre: Man ersetze einfach die Ladungen durch die Massen…
Haller: … wobei allerdings noch die Gravitationskonstante G eine Rolle spielt, die Sie in die Physik eingeführt haben.
Newton: Selbstverständlich ist die Kenntnis der Masse allein nicht genug. Meine Gravitationskonstante drückt aus, wie groß die Massenanziehung zwischen zwei Körpern in der Entfernung von einem Meter ist, wenn beide Körper die Masse von einem Kilogramm besitzen. Übrigens war zu meiner Zeit diese Konstante noch mit einer großen Ungenauigkeit behaftet. Was ist denn der heutige Zahlenwert?
Haller: Im Vergleich zu anderen Naturkonstanten ist die Newtonsche Gravitationskonstante auch heute noch nicht sehr genau bekannt. Der heutige Wert ist 6,67259·10-11 m3kg-1s-2. Dies bedeutet, daß die Massenanziehung zwischen den beiden von Ihnen erwähnten Körpern eine gegenseitige Beschleunigung der Körper von 6,67259·10-11 ms-2 verursacht. In einer Sekunde nimmt also die relative Geschwindigkeit der Körper um nur etwas mehr als 60 Billionstel Meter pro Sekunde zu. Im Vergleich dazu ist die Zunahme der Geschwindigkeit desselben Körpers im Schwerefeld der Erde in der Sekunde fast 10 Meter pro Sekunde.
Newton: Ich möchte noch daran erinnern, daß die elektrische Kraft eine Folge der Existenz des elektrischen Kraftfeldes ist, das jeden elektrisch geladenen Körper umgibt, das aber sonst ein eigenständiges Gebilde ist, also eine Eigenschaft des Raumes, die den gela-
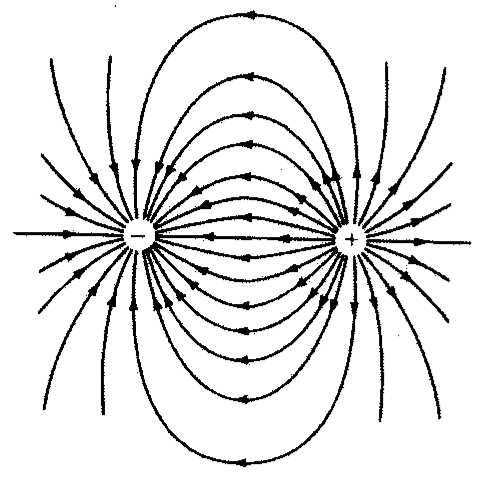
Abb. 3-2 Zwei ungleichnamig geladene Körper ziehen sich an. Dies ist die Folge der elektrischen Kraftfelder, die die Körper umgeben. Gezeigt ist hier der Verlauf der Feldlinien. Die beiden Körper ziehen sich zusätzlich durch ihre Gravitation an. Letztere ist jedoch viele Größenordnungen schwächer als die elektrische Kraft. Beide Kraftwirkungen haben aber eines gemeinsam: Die Stärke der Kräfte nimmt mit dem Quadrat des Abstandes ab.
denen Körper umgibt, ihm gewissermaßen eine zusätzliche Eigenschaft verleiht. Ein Punkt im Raum ist also nicht nur ausgezeichnet durch seine Koordinaten bezüglich Raum und Zeit, sondern auch durch die Angabe der Stärke des elektrischen Feldes. Ein Raumgebiet, das von elektrischen Feldern angefüllt ist, ist reicher an Struktur, sozusagen weniger leer, als ein Raumgebiet ohne Feld. Mit der Gravitation könnte es ja ganz ähnlich sein. Ein Körper ist umgeben von seinem Gravitationsfeld, das dann eine ganz ähnliche Rolle wie das elektrische Feld spielt. In einem Buch las ich, daß im vorigen Jahrhundert diese Analogie zwischen Gravitation und Elektrizität benutzt wurde, um Vermutungen über das elektrische Kraftgesetz anzustellen. Bevor man das vom Experiment her wußte, hat man also bereits spekuliert, daß sich die elektrische Kraft ebenso wie die Gravitationskraft verhält, also mit dem Quadrat des Abstandes schwächer wird. Für mich heißt das: Elektrische und gravitative Felder sind vermutlich völlig analog.
Haller: Nicht ganz – vergessen Sie nicht die Tatsache, daß die Massenanziehung im allgemeinen doch viel schwächer als die elektrische Kraft ist, geradezu winzig. Dies hängt natürlich von den Ladungen ab. Aber wenn wir einmal die elektrische Anziehung zwischen einem Proton und einem Elektron im Atom des Wasserstoffs vergleichen mit der gravitativen Anziehung zwischen den beiden, dann ergibt sich, daß die Massenanziehung um einen Faktor 1038 mal schwächer ist als die elektrische Anziehung, also so viel wie hundertmal eine Billion mal eine Billion mal eine Billion. Man kann also die Gravitation im Vergleich zur elektrischen Kraft vorerst völlig vergessen.
Daß dies makroskopisch augenscheinlich nicht der Fall ist, liegt ja nur daran, daß die makroskopischen Körper, etwa diese Tasse hier, nach außen hin elektrisch neutral sind. Aber selbst bei elektrisch aufgeladenen makroskopischen Körpern ist die elektrische Ladung immer sehr klein im Vergleich zu den vielen elektrisch geladenen Atomteilchen im Innern des Körpers. Wäre dies nicht so, dann würden die elektrischen Kräfte enorm stark sein. Denken Sie an einen Uranatomkern, der 92 elektrisch geladene Protonen enthält. Die elektrischen Abstoßungskräfte im Uran sind so stark, daß sie die wirkenden Kernkräfte fast genau aufheben. Ein kleiner Stoß von außen, etwa durch die Kollision eines Teilchens mit dem Kern, und schon fliegt der Urankern auseinander – ein Prozeß, der ja in einem Kernreaktor zur Energieerzeugung technisch ausgenutzt wird.
Die Tatsache, daß die elektrische Kraft so viel stärker als die Gravitation ist, könnte durchaus ein Hinweis sein, daß die Gravitation ein qualitativ anderes Phänomen ist als die Elektrizität, und genau diese Idee wird in Einsteins Theorie der Gravitation realisiert, wie wir wohl bald sehen werden.
Einstein: Noch etwas, Sir Isaac. Es gibt einen wichtigen Unterschied zwischen der elektrischen Kraft und der Gravitationskraft. Bei den elektrischen Kräften gibt es sowohl Anziehung wie Abstoßung, je nachdem, ob gleichnamige Ladungen oder ungleichnamige vorliegen, bei der Gravitation gibt es das nicht. Massen ziehen sich immer nur an. Eine Abstoßung, also eine Art Antigravitation, existiert nicht, auch wenn dies in irgendwelchen »Science fiction«- Büchern oftmals behauptet wird.
Newton: Wenn Sie schon dieses seltsame Wort Antigravitation ins Spiel bringen – so sicher bin ich mir nicht, ob es nicht doch so etwas gibt. Als wir vor einiger Zeit am CERN bei Genf zusammentrafen, war von Antiteilchen die Rede. Zu jeder Teilchenart in der Natur gibt es ein Antiteilchen, etwa das Antiproton zum Proton. Wie steht es denn mit der Gravitation bei den Antiteilchen? Es könnte doch sein, daß sich ein Proton und ein Antiproton gravitativ nicht anziehen, sondern abstoßen. In meiner Gravitationstheorie würden die Antiteilchen gewissermaßen mit negativer Masse erscheinen, dem Analogon der negativen elektrischen Ladung. Dann hätten wir eine Antigravitation neben der üblichen Gravitation. Da die normale Materie aus Teilchen besteht und nicht aus Antiteilchen, würde sich für die normalen gravitativen Erscheinungen im Kosmos keine Änderung ergeben, wohl aber genau dann, wenn Antimaterie ins Spiel kommt. Zwei Sterne, der eine aus Materie, der andere aus Antimaterie, würden sich also nicht anziehen, sondern abstoßen – das wäre ein imposantes Schauspiel im Kosmos.
Einstein: Das würde mich denn schon wundern. Jedenfalls wäre dies im Rahmen meines Zugangs zur Gravitation unmöglich.
Newton: Ihre Theorie in Ehren, aber sie könnte ja, mit Verlaub, auch falsch oder zumindest nur für die normale Materie gültig sein. Wir reden hier schließlich nicht über Politik oder Kunst, sondern über Physik – das letzte Wort hat immer das Experiment, und das ist am Ende immer eindeutig. Das ist ja das Gute in unserer Wissenschaft – faule Kompromisse gibt es nicht, und schwammige oder irreführende Begriffe werden über kurz oder lang eliminiert. Also, was weiß man vom Experiment hierzu, Mr. Haller? Entweder fallen die Antiteilchen nach oben oder nach unten, tertium non datur.
Haller: Sie treffen da eine wunde Stelle – leider ist die Physik in diesem Punkt nicht ganz so eindeutig, wie Sie sich das wohl wünschen. Am CERN, von wo ich gerade herkomme, gibt es zwar eine Menge Antiprotonen, mit denen man eine ganze Reihe von Experimenten anstellt. Aber was ihre Gravitation anbelangt – viel weiß man da leider nicht, genaugenommen gar nichts. Es gibt Pläne, ein Fallexperiment mit Antiprotonen durchzuführen, aber ob es in absehbarer Zeit dazu kommen wird, vermag ich nicht zu sagen. Die Schwierigkeiten sind groß, denn Antiprotonen leben bei Experimenten nicht lange, da sie leicht mit der umgebenden Materie in Reaktion treten können und auf diese Weise vernichtet werden. Allerdings gibt es indirekte theoretische Argumente, die dagegen sprechen, daß bei den Antiteilchen eine Antigravitation wirksam werden könnte. Man weiß nämlich, daß die Masse der Protonen sich aus mehreren Teilen zusammensetzt, darunter einem Teil, der mit den Antiteilchen zu tun hat, genauer gesagt mit Antiquarks. Die Quarks sind die kleinsten Teilchen der subnuklearen Materie und agieren als die Bausteine der Kernteilchen. Im Proton gibt es vornehmlich Quarks, im Antiproton vornehmlich Antiquarks. Jedoch ist es seit den siebziger Jahren bekannt, daß im Proton auch Antiquarks vorkommen, übrigens eine Folge der sehr starken Kräfte zwischen den Quarks und von Einsteins Spezieller Relativitätstheorie. Aus diesem Grunde rührt ein Teil der Masse des Protons – man schätzt etwa 10 Prozent – von Antiquarks her, ist also Masse von Antimaterie. Nun weiß man aber, daß es die Gesamtmasse des Protons ist, die die Massenanziehung bestimmt, also auch in Ihre Gravitationsgleichung eingeht, einschließlich der Masse, die von der Antimaterie im Innern des Protons herrührt. Damit ist es im Grunde nicht möglich, daß die Antimaterie andere Gravitationseigenschaften haben könnte als die normale Materie. Trotzdem – das Argument ist indirekt, und mir wäre wohler, wenn man direkt beobachten würde, daß Antimaterie im Schwerefeld der Erde ebenso fällt wie normale Materie und nicht etwa von der Erde abgestoßen wird. Nichtsdestotrotz – wir können wohl mit einiger Sicherheit davon ausgehen, daß es abstoßende Kräfte bei der Gravitation nicht gibt. Für Sie, Einstein, kann das nur gut sein, denn eine Antigravitation der Antiteilchen wäre das Ende Ihrer Theorie; denn ich wüßte nicht, wie man diese in Ihre Vorstellungen einbauen könnte – warum das so ist, wird bald klarwerden, denke ich.
Einstein: Mehr noch – ich bin ziemlich sicher, in Kürze werden Sie, Mr. Newton, die Antigravitation genau so unerquicklich finden wie ich. Übrigens hat Lichtenberg, der große Göttinger Experimentalphysiker, in seinen Vorlesungen gern betont, daß das elektrische Kraftgesetz allgemeiner ist und auch auf das menschliche Verhalten übertragen werden kann: Personen, die sich einst als ungleichnamig sehr stark angezogen haben, stoßen sich zuweilen einander heftig ab, sobald sie gleichnamig geworden sind – also nach einer Heirat. Gottlob scheint dies bei der Gravitation nicht der Fall zu sein. Gravitativ zu heiraten ist also viel lobenswerter und aussichtsreicher als auf elektrischem Wege.
Newton: Das ist ja das Besondere an meinem Gravitationsgesetz: Es gibt eben nur eine Anziehung, wenn es nur positive Massen gibt. Wenn es in der Tat keine Antigravitation gibt – das wollen wir mal jetzt voraussetzen, denn Hallers Argument bezüglich der Antiquarks im Proton hat mich zwar nicht völlig überzeugt, scheint mir aber sehr plausibel -, dann liegt das einfach daran, daß es nur eine Art Masse gibt. Massen sind eben immer positiv, auch die Massen der Antiteilchen. Aber abgesehen von dieser Tatsache, die zweifellos einen wesentlichen Unterschied zwischen der Gravitation und der Elektrizität beschreibt, sind die elektrischen und die gravitativen Kräfte einander ähnlich. Deswegen denke ich, daß die Relativitätstheorie zwar neue, interessante Aspekte des Gravitationsphänomens aufzudecken vermag, wie sie es bei den elektrischen und magnetischen Erscheinungen ja auch getan hat, jedoch nichts grundsätzlich Neues beisteuern kann. Elektrische Ladungen und Massen gibt es schließlich auch ohne die Relativitätstheorie. Deshalb verwahre ich mich dagegen, lieber Kollege Einstein, wenn Sie, wie vorhin getan, wie selbstverständlich von einer Art Einheit von Raum, Zeit und Gravitation reden, so als sei die Gravitation eine Folge der Raum-Zeit-Struktur. Die elektrischen Phänomene haben schließlich auch nichts mit der Raum-Zeit-Struktur zu tun.
– Einstein erhob sich, ging ans Fenster und blickte eine Weile nachdenklich auf den nahen Havelsee. Nach einer kurzen Pause drehte er sich um, ging auf Newton zu und schaute ihn mit seinen großen Augen aufmerksam und wohlwollend an.
Einstein: Lieber Freund, halten Sie sich jetzt ganz fest. Es stimmt – die Gravitation ist tatsächlich das, was Sie gerade selbst sagten: eine Manifestation der Struktur von Raum und Zeit. Die gravitative Kraft zwischen massiven Körpern ist im Gegensatz zur elektrischen Kraft keine selbständige Naturkraft, sondern ein Ausfluß der Geometrie von Raum und Zeit. Dies und nichts anderes ist die Quintessenz meiner Allgemeinen Relativitätstheorie, die ich hier in Berlin im Jahre 1915 vollendete.
– Noch während Einstein sprach, war Newton aufgesprungen und unruhig im Zimmer auf- und abgegangen. Er war sichtlich erregt.
Newton: Aber das ist doch völlig absurd. Wie können Sie behaupten, daß eine physikalische Kraft, die wir alle zu jeder Zeit spüren, die uns hier auf dem Fußboden hält, etwas mit der Geometrie der Raum-Zeit zu tun hat? Raum ist Raum, und Kraft ist Kraft, Einstein, beide sind so verschieden wie Feuer und Wasser.
– Newton nahm einen Apfel, der in einer Schale auf dem Tisch lag, und ließ ihn auf den Holzboden fallen.
Newton: Hier sehen Sie es selbst. Der Apfel fällt nach unten, weil er von der Erde angezogen wird – eine Konsequenz des Gravitationsgesetzes. Sie können doch nicht behaupten, lieber Herr Kollege, daß diese Kraft nicht real sei, sondern eine Einbildung – eine Folge der Struktur von Raum und Zeit – welch eine Absurdität. Wollen Sie vielleicht behaupten, der Apfel fällt nach unten, weil es durch eine komplizierte Struktur von Raum und Zeit so erzwungen wird? Wie wir wissen, ist Ihre Relativitätstheorie ja nur relevant, wenn die Geschwindigkeiten der beteiligten Objekte nahe der Lichtgeschwindigkeit c liegen. Dies ist ja hier nicht der Fall – der Apfel fiel gerade nach unten mit einer im Vergleich zu c geradezu lächerlich kleinen Geschwindigkeit von nur einigen Metern in der Sekunde, und wir selbst, die wir den Vorgang beobachtet haben, waren in Ruhe. Für solche Situationen gelten meine Gesetze, aufgeschrieben in den »Principia«. Also was soll dann Ihr Gerede von der Relativitätstheorie, sei es nun die Spezielle oder die Allgemeine!
Einstein: Genau wie Sie jetzt, Newton, so haben sich seinerzeit meine Kollegen in Berlin verhalten, als ich am 15. November 1915 meine Allgemeine Relativitätstheorie, also meine Theorie der Gravitation, der Akademie vorstellte. Vermutlich haben einige von ihnen insgeheim gedacht, der Einstein sei diesmal ganz verrückt geworden, aber die meisten dachten sicherlich, ich befände mich auf dem Holzweg und würde meinen Irrtum bald einsehen.
Newton: Nun gut – wollen wir also zu Ihren Gunsten annehmen, daß dem nicht so ist, denn irgendwas wird an Ihrer Theorie doch wohl dran sein. Ich schlage vor, wir gehen die Dinge etwas systematischer an. Zurück zur Elektrizität. Wie wir gesehen haben, spielen Masse und elektrische Ladungen analoge Rollen in unserem physikalischen Drama. Trotzdem scheint mir diese Analogie etwas vordergründig zu sein. Die Masse eines Körpers und seine elektrische Ladung sind zwei recht verschiedene Dinge, so wie ich das sehe. Wird nicht die Ladung von speziellen Ladungsteilchen getragen, während die Masse schlichtweg eine Eigenschaft aller Teilchen ist, zumindest aller derjenigen Teilchen, die überhaupt eine Masse besitzen?
Haller: Da haben Sie vollkommen recht. Jeder Körper besteht aus Atomen, die ihrerseits aus Atomkernen und aus Elektronen in den Atomhüllen bestehen. Die Elektronen sind elektrisch geladen. Jedes Elektron besitzt die gleiche elektrische Ladung, die man als negativ bezeichnet. Übrigens ist diese Bezeichnung willkürlich eingeführt worden, und zwar schon im 18. Jahrhundert von dem amerikanischen Naturforscher Benjamin Franklin. Er hätte sie ebenso als positiv bezeichnen können, was sogar im nachhinein vernünftiger gewesen wäre – aber danach ist man immer klüger. Was bemerkenswert ist: Die Größe dieser Ladung ist eine Naturkonstante, die allgemein einfach als die elektrische Elementarladung bezeichnet wird. Alle elektrisch geladenen Objekte, die in der Natur vorkommen, besitzen eine Ladung, die ein ganzzahliges Vielfaches der Elementarladung darstellt.
Newton: Hm. Hat denn die elektrische Ladung der Atomkerne, die ja dann positiv ist, auch etwas mit den Elektronen und deren Ladung zu tun?
Haller: Eigentlich nicht, die Atomkerne bestehen ja aus Protonen und Neutronen. Die Protonen sind positiv geladen, die Neutronen
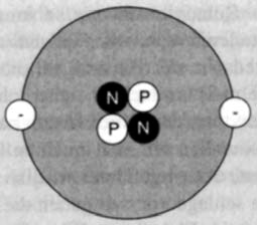
Abb. 3-3 Schematisches Bild eines Heliumatoms. Der Atomkern besteht aus zwei Protonen und zwei Neutronen, die Hülle aus zwei Elektronen. Das Atom ist als Ganzes elektrisch neutral. sind neutral, haben also keine Ladung. Nach außen hin sind die Atome elektrisch neutral, da die positive Ladung des Kerns von der negativen Ladung der Elektronen in der Hülle aufgehoben wird. Zum Beispiel besteht das einfachste Atom, also das des Wasserstoffs, aus einem Proton als Kern und einem Elektron in der Hülle. Die Ladung des Protons ist genauso groß wie die Elektronladung, nur ist erstere eben positiv, die andere negativ.
Newton: Moment mal. Sie behaupten, die Kernladung, also beim Wasserstoff die Protonladung, hat nichts mit der Elektronladung zu tun?
Einstein: Aber nein. Protonen und Elektronen sind ja ganz verschiedene Teilchen.
Newton: Ist es dann nicht merkwürdig, daß ihre Ladungen gleich sind? Vielleicht sind ihre Ladungen doch etwas verschieden, sagen wir ein Prozent oder sogar weniger. Dann würden die Atome eine wenn auch kleine elektrische Ladung besitzen. Wie gut weiß man denn, daß die Ladungen beider Teilchen, abgesehen vom Vorzeichen, wirklich gleich sind?
Haller: Da muß ich Sie enttäuschen, Sir Isaac. Sie haben aber durchaus recht – im Prinzip könnte es sehr wohl sein, daß die elektrischen Ladungen des Protons und des Elektrons etwas verschieden sind. Das hätte aber geradezu katastrophale Folgen, denn dann müßten sich die Atome, die eine wenn auch kleine Ladung besäßen, gegenseitig abstoßen. Die Folge wäre, daß sich größere Materieansammlungen, etwa Sterne oder Planeten, gar nicht bilden könnten. Würde plötzlich, sagen wir im Bruchteil einer Sekunde, die Protonladung etwas kleiner als die Elektronladung, wären die Folgen katastrophal. Alle Körper würden explodieren. Unsere Erde würde sich sofort in einen riesigen Gasball verwandeln, der sich nach allen Richtungen schnell ausbreitet.
Newton: Natürlich – hätte ich mir denken können. Damit ist klar – die Stabilität der Stoffe unserer makroskopischen Welt macht es unabdingbar -, daß Proton- und Elektronladung völlig gleich sind.
Einstein: Seltsam – das kann doch wohl kein Zufall sein. Sie beschäftigen sich doch auch mit den Elementarteilchen, Haller. Können Sie mir sagen, woher ein Proton weiß, daß seine elektrische Ladung genauso groß sein muß wie die eines Elektrons, abgesehen vom Vorzeichen natürlich? Beide Teilchen haben ja wohl kaum etwas miteinander zu tun, zumal das Proton auch noch aus Quarks besteht, im Gegensatz zum Elektron. Sie unterscheiden sich also mindestens so wie Äpfel und Blaubeeren.
Haller: Also gut, wenn Sie schon auf diesem Punkt herumreiten wollen: Protonen und Elektronen haben zunächst einmal wirklich nichts miteinander zu tun. Es ist legitim zu fragen, warum denn dann ihre elektrischen Ladungen genau gleich sind. Diese, ich gebe zu, merkwürdige Eigenschaft hat heute einen eigenen Namen. Man bezeichnet sie als die Universalität der Ladung – manchmal redet man auch etwas gezierter von der Quantisierung der elektrischen Ladung.
Einstein: Dem Ding einen Namen zu geben ist eine Sache, es zu verstehen eine andere. Also raus mit der Sprache, Haller. Wißt ihr nun, warum die Ladungen gleich sind, oder wißt ihr es nicht?
Haller: Wenn Sie mich schon so direkt fragen – man weiß es heute auch nicht. Es war und ist ein Rätsel. Die meisten Teilchenforscher nehmen an, daß die Protonen und Elektronen letztlich doch miteinander verwandt sind, obwohl sie sich vordergründig als so verschieden darstellen. Die Universalität der Ladung wäre dann sozusagen das äußere Kennzeichen dieser Verwandtschaft, der gemeinsame Ehering, der sie verbindet.
Einstein (zu Newton): Sie sehen also, die Physiker kochen heute auch nur mit Wasser. Bis heute kennen sie nicht den genauen Grund, warum das Wasserstoffatom keine Ladung besitzt – ist das nicht ein Skandal?
Haller: Es tut mir leid, daß ich nicht mit einer befriedigenden Lösung aufwarten kann. Aber ich kann Ihnen versichern, es handelt sich hier um eine besonders harte Nuß, die der Herrgott uns da zum Knacken gegeben hat.
Einstein: Ist schon gut, Haller. Es ist ja auch ganz schön zu wissen, daß man noch nicht alles weiß. Irgendwann wird man den wahren Grund erfahren. Sie wissen ja, raffiniert ist der Herrgott, aber boshaft ist er nicht. Es ist nur schade, daß Newton und ich da nicht mitspielen können. Aber gut – lassen wir das jetzt auf sich beruhen – gottlob spielt das Ladungsproblem für die Gravitation vordergründig erst mal keine wichtige Rolle.
Newton: Die elektrische Ladung eines Objekts, falls es überhaupt eine solche trägt, ist gewissermaßen die Quelle der elektrischen Kraft, die von dem Objekt ausgeht. Wie wir jetzt wissen, sind diese Quellen die Ladungen der Elektronen oder Protonen, aus denen sich das Objekt zusammensetzt. Analog ist die Quelle der Gravitationskraft die Masse des Objekts, also im Falle eines Elektrons die Masse des Elektrons.
Haller: Man könnte die Masse eines Teilchens durchaus als die Gravitationsladung des Teilchens bezeichnen.
Newton: Genau. Nur gibt es im Fall der Gravitation aber nicht die im Grunde unverstandene Universalität der Ladung, von der wir gerade sprachen. Ein Elektron hat eine bestimmte Masse…
Einstein: Wenn man die Masse in Energieeinheiten ausdrückt, etwa in Megaelektronenvolt, entsprechend meiner Gleichwertigkeit von Masse und Energie, dann sind das 0,511 MeV.
Newton: Und das Proton ist fast genau 1836 mal schwerer als das leichte Elektron – es hat die Masse von 938 MeV. Das heißt dann, daß im Gravitationsfeld auf einem Proton eine Kraft wirkt, die 1836 mal stärker ist als im Falle eines Elektrons. Von einer Art Universalität der Gravitationskraft analog zum elektrischen Fall kann also keine Rede sein. Die Kraft auf ein Teilchen hängt von der Masse ab, und da die verschiedenen Teilchen verschiedene Massen haben, sind die einzelnen Kraftwirkungen auch ganz verschieden. Was ist die Ursache dieses seltsamen Phänomens? Was ist überhaupt die Ursache dafür, daß sich Körper mit Masse gegenseitig anziehen?
– Einstein hatte sich während dieser Worte Newtons erhoben und war zum Bücherschrank gegangen. Er nahm ein Buch zurHand und schlug es auf.
Einstein: Sehr verehrter Herr Kollege Newton, genau diese Frage habe ich mir im Jahre 1906 gestellt, übrigens, wie ich meine, ganz auf Ihren Spuren wandelnd. Ich erlaube mir, Sie aus Ihren »Principia« zu zitieren. Gegen Ende Ihres Buches schreiben Sie: »Ich habe bisher die Erscheinungen der Himmelskörper und die Bewegungen des Meeres durch die Kraft der Schwere erklärt, aber ich habe nirgends die Ursache der letzteren angegeben. Diese Kraft rührt von irgendeiner Ursache her, welche bis zum Mittelpunkt der Sonne und der Planeten dringt, ohne irgend etwas von ihrer Wirksamkeit zu verlieren. Sie wirkt nicht nach Verhältnis der Oberfläche derjenigen Teilchen, worauf sie einwirkt (wie die mechanischen Ursachen), sondern nach Verhältnis der Menge fester Materie, und ihre Wirkung erstreckt sich nach allen Seiten hin, bis in ungeheure Entfernungen, indem sie stets im doppelten Verhältnis der letzteren abnimmt. Die Schwere gegen die Sonne ist aus der Schwere gegen jedes ihrer Teilchen zusammengesetzt, und sie nimmt mit der Entfernung von der Sonne genau im doppelten Verhältnis der Abstände ab… Ich habe noch nicht dahin gelangen können, aus den Erscheinungen den Grund dieser Eigenschaften der Schwere abzuleiten, und Hypothesen erdenke ich nicht.« Sie schreiben also, daß Sie keine Hypothesen machen, aber in diesem Punkt, lieber Newton, traue ich Ihnen nicht. Ich bin sicher, daß Sie damals kräftig an Hypothesen gedrechselt haben.
Newton: Jetzt braucht es ja kein Geheimnis mehr zu bleiben – in der Tat, Hypothesen habe ich ersonnen, nur waren die meiner Meinung nach nicht recht befriedigend. Wenn ich Sie kürzlich recht verstanden haben, ist Ihre Allgemeine Relativitätstheorie ja auch so etwas. Das Problem, an dem ich immer scheiterte, war die Tatsache, daß die Ursache der Gravitation, falls man von einer solchen überhaupt sprechen kann, wie ich schrieb, überall präsent ist, also ohne weiteres bis ins Innere der Sonne oder der Planeten vordringen kann. Nachdem ich jetzt einiges über elektrische Phänomene weiß, ist dies noch seltsamer. Elektrische Kräfte kann man ja ohne weiteres abschirmen, wie man weiß, aber die Gravitation durchdringt alles, wie der Raum selbst.
Einstein: Ich hoffe schon, daß meine Theorie mehr als eine Hypothese ist. Immerhin wird sie heutzutage als die Theorie der Gravitation bezeichnet.
Newton: Da wollen wir doch erst einmal abwarten. Solange ich nicht weiß, was die Grundgedanken Ihrer Theorie sind, kann ich dem nicht zustimmen.
Haller: Seien Sie nicht so skeptisch, Mr. Newton – in ein paar Tagen werden Sie, dessen bin ich mir sicher, ganz anders über Einsteins Theorie reden. Übrigens sagten Sie gerade etwas sehr Interessantes: Sie sagten, die mögliche Ursache der Gravitation durchdringt alles, wie der Raum selbst. Wenn es gelänge, die Struktur des Raumes für die Gravitation verantwortlich zu machen, oder vielleicht die Struktur von Raum und Zeit, dann könnte man leicht verstehen, warum die Gravitation nicht abzuschirmen ist,

Abb. 3-4 Ein Proton und ein Neutron verbinden sich als Folge der starken Kernkraft zu einem Deuteron, dem Atomkern des schweren Wasserstoffs. Die Masse des gebundenen Kernsystems ist etwas geringer als die Summe des Protons und des Neutrons.
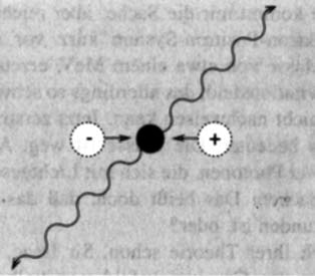
Abb. 3-5 Die Zerstrahlung von Elektron und Positron in zwei Photonen.
denn der Raum oder die Zeit lassen sich nicht abschirmen. Genau dies ist in Einsteins Theorie der Fall, wie wir bald sehen werden. Aber zurück zu der Analogie zwischen Masse und Ladung, über die wir vorher sprachen. Es gibt noch einen wichtigen Unterschied zwischen beiden Begriffen, den wir bisher noch nicht erwähnt haben. Bei jedem physikalischen Prozeß bleibt die elektrische Ladung unverändert – sie ist streng erhalten. Dies gilt jedoch nicht für die Masse. Bei vielen physikalischen Prozessen, insbesondere bei den Prozessen der Kern- und der Teilchenphysik, ist die Gesamtmasse der beteiligten Teilchen oder Kerne nicht erhalten.
Newton: Sie haben recht – das ist in der Tat ein wichtiger Unterschied. Wenn wir ein Proton und ein Neutron zu einem Atomkern zusammenfügen, also zum Atomkern des schweren Wasserstoffs, dann ist die Masse des neu entstandenen Kerns etwas kleiner als die Summe der Massen von Proton und Neutron.
Haller: Noch eindrucksvoller sieht man das bei der Vernichtung von Materie und Antimaterie. Wenn wir ein Elektron und sein Antiteilchen, das Positron, zusammenbringen, zerstrahlen die beiden Teilchen in zwei Photonen. Die Ausgangsteilchen in diesem Prozeß besaßen eine Gesamtmasse von etwa einem MeV – nach der Zerstrahlung findet man nur die beiden Photonen vor, die selbst keine Ruhemasse besitzen.
Newton: Jetzt kommt mir die Sache aber reichlich merkwürdig vor. Ein Elektron-Positron-System kurz vor der Vernichtung besitzt eine Masse von etwa einem MeV, erzeugt also in seiner Nähe ein Gravitationsfeld, das allerdings so schwach ist, daß man es praktisch nicht nachweisen kann. Jetzt zerstrahlen die beiden Teilchen. Das bedeutet: Die Masse ist weg. Alles, was übrigbleibt, sind zwei Photonen, die sich mit Lichtgeschwindigkeit auf und davon machen. Das heißt doch, daß das Gravitationsfeld auch verschwunden ist, oder?
Einstein: Nach Ihrer Theorie schon, Sir Isaac, denn nach Ihrer Vorstellung ist das Gravitationsfeld unmittelbar an die Masse gekoppelt. Nur – Sie werden mir zugeben, es ist schon etwas seltsam, wenn das Gravitationsfeld bei der Zerstrahlung ganz plötzlich nicht mehr da ist. Finden Sie nicht?
Newton: Sehr merkwürdig. Ehrlich gesagt, ich bin etwas verwirrt. Zwar bin ich schon der Meinung, daß mit dem Gravitationsfeld, das von dem Elektron-Positron-System ausgeht, etwas passiert, nur sollte es nicht so abrupt verschwinden. Ich denke, daß hier etwas mit meiner Theorie nicht ganz stimmen kann.
Einstein: Endlich, Mr. Newton. Mit diesem Beispiel der Zerstrahlung haben wir sozusagen die Achillesferse Ihrer Theorie getroffen. Wir werden später sehen, daß in meiner Theorie die Sache nicht ganz so dramatisch abläuft,
Newton: Sie machen das ja ganz spannend, lieber Herr Kollege. Ich gebe also zu, daß meine Theorie der Gravitation offensichtlich nicht so perfekt funktionieren kann, sobald exotische Phänomene wie die Zerstrahlung von Materie und Antimaterie betrachtet werden, von denen ich beim Schreiben der »Principia« nichts wußte. Vermutlich ist es noch zu früh, die Diskussion dieser Angelegenheit zu einem Ende zu bringen. Aber ich merke mir es vor – später müssen wir unbedingt darauf zurückkommen.
Einstein: Und ob. Sie werden staunen, wie einfach die Sache in meiner Theorie sein wird.
Haller (auf die Uhr schauend): Meine Herren, Mittag nähert sich. Ich glaube, für den Augenblick haben wir genug Probleme gewälzt. Ich schlage vor, wir setzen unsere Diskussion nach dem Mittagessen fort.
Kurze Zeit später konnte man die drei Physiker beobachten, die Einsteins Haus verließen, hinunter zum See gingen und ein nahe gelegenes Fischrestaurant betraten.